In CS61B, you learned about many different sorting algorithms. Why are we learning yet another new one in this class? All of the traditional sorting algorithms (i.e. quick sort, insertion sort, etc.) rely on us being able to store all of the data in memory. This is a luxury we do not have when developing a database. In fact, most of the time our data will be an order of magnitude larger than the memory available to us.

I/O Review

Remember that we incur 1 I/O any time we either write a page from memory to disk or read a page from disk into memory. Because of how time consuming it is to go to disk, we only look at the number of I/Os an algorithm incurs when analyzing its performance instead of traditional measures of algorithmic complexity like big-O. Therefore, when developing our sorting algorithm we will attempt to minimize the number of I/Os it will incur. When counting I/Os, we ignore any potential caching done by the buffer manager. This implies that once we unpin the page and say that we are done using it, the next time we attempt to access the page it will always cost 1 I/O. Think of this as the buffer manager evicting the data page from the buffer pool once the data page is no longer being used.

Two Way External Merge Sort

Let’s start by developing a sorting algorithm that works but is not as good as possible. Because we cannot keep all of our data in memory at one time, we know that we are going to sort different pieces of it separately and then merge it together.

In order to merge two lists together efficiently, they must be sorted first. This is a hint that the first step of our sorting algorithm should be to sort the records on each individual page. We’ll call this first phase the “conquer” phase because we are conquering individual pages.

After this, let’s start merging the pages together using the merge algorithm from merge sort. We’ll call the result of these merges sorted runs. A sorted run is a sequence of pages that is sorted.

The rest of the algorithm will simply be to continue merging these sorted runs until we have only one sorted run remaining. One sorted run implies that our data is fully sorted! See the image on the next page for a diagram of the algorithm run to completion.

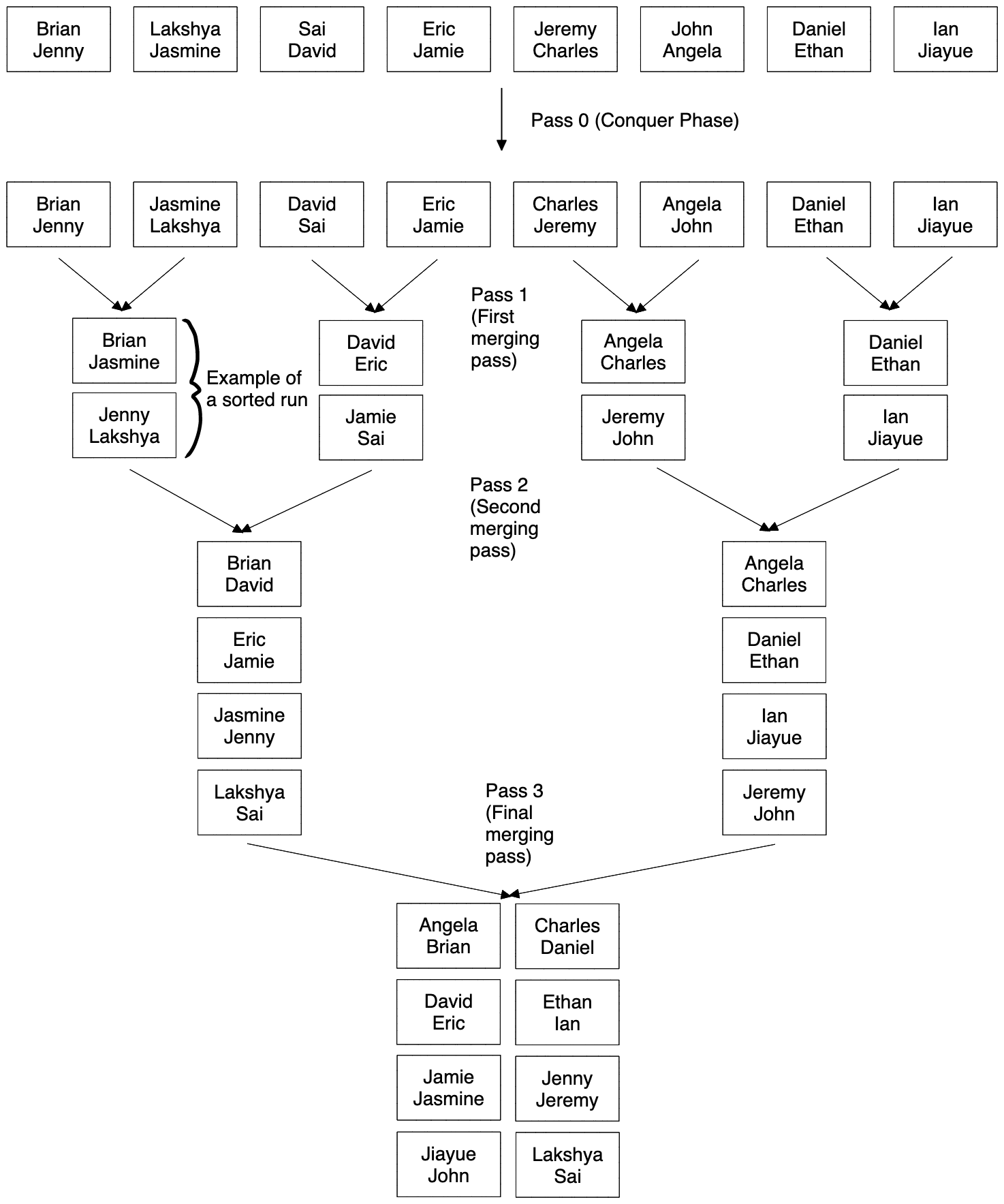
Analysis of Two Way Merge

When analyzing a database algorithm, the most important metric is the number of I/Os the algorithm takes, so let’s start there. First, notice that each pass over the data will take \(2 * N\) I/Os where \(N\) is the number of data pages. This is because for each pass, we need to read in every page and write back every page after modifying it.

The only thing left to do is to figure out how many passes we need to sort the table. We always need to do that initial “conquer” pass, so we always have at least one. Now, how many merging passes are required? Each pass, we cut the amount of sorted runs we have left in half. Dividing the data each time should scream out log to you, and because we’re diving it by 2, the base of our \(\log\) will be 2. Therefore we need \(\lceil \log_2(N) \rceil\) merging passes, and \(1 + \lceil\log_2(N)\rceil\) passes in total. This leads to our final formula of \(2N * (1 + \lceil\log_2(N)\rceil)\) I/Os. (Note: Pass 0, the initial conquer pass, counts as a pass in external sorting and is included as one of the passes in this formula for I/O cost).

Now let’s analyze how many buffer pages we need to execute this algorithm. Remember that a buffer page, or buffer frame, is a slot for a page in memory.

The first pass, the “conquering pass”, sorts each page individually. This means we only ever need 1 buffer page for this pass, to hold the page that we are sorting!

Now let’s analyze the merging passes. Recall how merging works in merge sort. We only compare the first value in each of the two lists that we are merging. This means that we only need to store the first page of each sorted run in memory, rather than the entire sorted run. When we have gone through all of the records from a page, we simply get rid of that page from memory and load in the next page of the sorted run. So far, we need 2 buffer pages (1 for each sorted run). We will call the buffer frame used to store the front of each sorted run the input buffer. The only thing we’re missing now is a place to store our output. We need to write out records somewhere, so we need 1 more page, called the output buffer. Whenever this page fills up, we flush it to disk and start constructing the next page. In total, we have two input buffers and 1 output buffer for a total of 3 pages required in each merging pass. We often have more than 3 pages available to use in memory for sorting, so this algorithm does not take advantage of all the memory that we have. Let’s construct a better algorithm that uses all of our memory.

Full External Sort

Let’s assume we have B buffer pages available to us. The first optimization we will make is in the initial “conquer pass.” Rather than just sorting individual pages, let’s load B pages and sort them all at once into a single sorted run. This way we will produce fewer and longer sorted runs after the first pass.

The second optimization is to merge more than 2 sorted runs together at a time. We have B buffer frames available to us, but we need 1 for the output buffer. This means that we can have B-1 input buffers and can thus merge together B-1 sorted runs at a time. See the diagram below of this sort assuming we have 4 buffer frames available to us.

Now we take in 4 (B) pages at a time during the conquering phase and output a sorted run of length 4. In the merging pass, we can merge all 3 (B - 1) sorted runs produced during the conquering pass at once. This cut the number of passes (and thus our I/Os) in half! Below is the general high-level flow of full external merge sort:

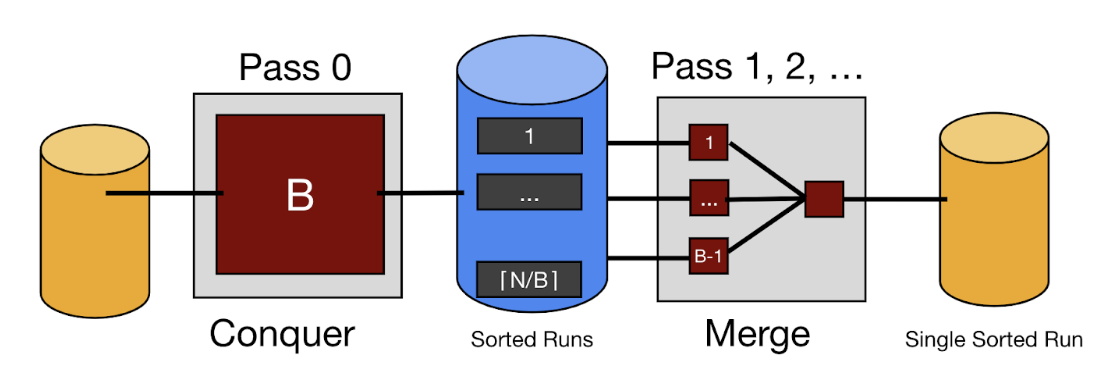
Analysis of Full External Merge Sort

Let’s now figure out how many I/Os our improved sort takes using the same process we did for Two-Way Merge. The conquering pass produces only \(\lceil N/B \rceil\) sorted runs now, so we have fewer runs to merge. During merging, we are dividing the number of sorted runs by \(B-1\) instead of 2, so the base of our log needs to change to \(B-1\). This makes our overall sort take \(1 + \lceil\log_{B-1}\lceil N/B\rceil\rceil\) passes, and thus \(2N * (1 + \lceil\log_{B-1}\lceil N/B\rceil\rceil)\) I/Os.

Practice Questions

1) You are trying to sort the Students table which has 1960 pages with 8 available buffer pages.
a. How many sorted runs will be produced after each pass?
b. How many pages will be in each sorted run for each pass?
c. How many I/Os does the entire sorting operation take?

2) What is the minimum number of buffer pages that we need to sort 1000 data pages in two passes?

3) You are trying to sort the Sailors table which has 200 pages. Suppose that during Pass 0, you have 10 buffer pages available to you, but for Pass 1 and onwards, you only have 5 buffer pages available.
a. How many sorted runs will be produced after each pass?
b. How many pages will be in each sorted run for each pass?
c. How many I/Os does the entire sorting operation take?

4) True or False: Increasing the number of buffer pages does not affect the number of I/Os performed in Pass 0 of an external sort.

5) True or False: Sorting an already sorted table takes fewer IOs than sorting a randomly-arranged table.

Solutions

1) The first pass loads all 8 buffer pages with data pages at a time and outputs sorted runs until each page is part of a sorted run. This means that we will have 1960 / 8 = 245 sorted runs of 8 pages after pass 0.

All subsequent passes merge 7 sorted runs at a time (remember we need a frame for the output buffer so we can only have B-1 input buffers) so after the first sorting pass we will have 245 / 7 = 35 sorted runs of 8 * 7 = 56 pages.

The next merging pass produces 35 / 7 = 5 sorted runs of 56 * 7 = 392 pages.

The next merging pass can merge all remaining sorted runs (because there are \(\le\) 7 sorted runs) so it will produce 1 sorted run of all 1960 pages.

Therefore the answer to a is: 245, 35, 5, 1 and the answer to b is: 8, 56, 392, 1960.

Each pass takes 2 * N I/Os where N is the total number of data pages because each page gets read and written in a pass. This means that the answer to c is: 4 * 2 * 1960 = 15,680 I/Os.

2) The conquer pass of sorting divides the number of sorted runs that we have by B (initially we consider each page to be its own sorted run even if it isn’t actually sorted yet). The merging pass divides the number of sorted runs by B-1. Together, two passes will divide the number of sorted runs we have by B(B-1). After those two passes we need to have one sorted run remaining, so we need: \(\frac{1000}{B(B-1)} \le 1\) You can move the denominator to the other side and then move 1000 over as well to get: \(B^2 - B - 1000 \ge 0\) Using the quadratic formula, you can get that B = 32.1 which means we need 33 buffer pages.

3) In Pass 0, we load data pages into all 10 buffer pages at a time and sort them to create sorted runs. Since we have 200 data pages, we will have 200/10 = 20 sorted runs after Pass 0 of 10 pages each.

In Pass 1, we can now only use 5 buffer pages. Here, we will merge sorted runs together, reserving 1 output buffer and designating the remaining 4 buffer pages as input buffers. Thus, we can merge 4 sorted runs at a time. Since we start with 20 sorted runs, we will end up with 20/4 = 5 sorted runs of 10 * 4 = 40 pages after Pass 1.

In Pass 2, we can merge up to 4 sorted runs at a time, so we will end up with 2 sorted runs (1 with 160 pages, 1 with 40 pages).

In Pass 3, we merge all remaining sorted runs, producing 1 sorted run of 200 pages.
Therefore the answer to a is: 20, 5, 2, 1 and the answer to b is: 10, 40, (160 and 40), 200.

Each pass takes 2 * N I/Os where N is the total number of data pages because each page gets read and written in a pass. This means that the answer to c is: (2 * 200 I/Os per pass) * 4 passes = 1600 I/Os.

4) True. Regardless of the number of buffer pages, every pass of an external sort (including Pass 0) performs the same number of IOs.

5) False. Regardless of how a table (of fixed length) is sorted, the sorting algorithm always takes the same number of IOs.